17+ D'Alembert Principle And Lagrange Equations Pdf
Angular momentum is a vector quantity more precisely a pseudovector that represents the product of a bodys rotational inertia and rotational velocity in radianssec about a particular axis. In this instance sometimes the term dynamics refers to the differential equations that the system satisfies eg Newtons second law or EulerLagrange equations and sometimes to the solutions to those.

Music A Mathematical Offering Dave Benson University Of Aberdeen
16 November 1717 29 October 1783 was a French mathematician mechanician physicist philosopher and music theoristUntil 1759 he was together with Denis Diderot a co-editor of the Encyclopédie.

. Differential equations first came into existence with the invention of calculus by Newton and LeibnizIn Chapter 2 of his 1671 work Methodus fluxionum et Serierum Infinitarum Isaac Newton listed three kinds of differential equations. Current models of particle physics imply that the earliest instance of gravity in the Universe possibly in the form of quantum gravity supergravity or a gravitational singularity along with ordinary space and time. 25 January 1736 10 April 1813 also reported as Giuseppe Luigi Lagrange or Lagrangia was an Italian mathematician and astronomer later naturalized FrenchHe made significant contributions to the fields of analysis number theory and both classical and.
The number π p aɪ. The term is properly understood as shorthand for the principle of inertia as described by Newton in his first law of motion. The principle of virtual work is used to study the static equilibrium of a system of rigid bodies however by introducing acceleration terms in Newtons.
It was traditionally believed to be related to the quantity of matter in a physical body until the discovery of the atom and particle physicsIt was found that different atoms and different elementary particles theoretically with the same amount of matter have nonetheless different massesMass in modern physics has multiple definitions which are. DAlemberts formula for obtaining solutions to the wave equation is named. Pierre-Simon marquis de Laplace l ə ˈ p l ɑː s.
23 March 1749 5 March 1827 was a French scholar and polymath whose work was important to the development of engineering mathematics statistics physics astronomy and philosophyHe summarized and extended the work of his predecessors in his five-volume Mécanique céleste Celestial. There are two main descriptions of motion. Hamiltons scientific career included the study of geometrical optics ideas from.
Passengers in a vehicle accelerating in the forward direction may perceive they are acted upon by a force. A fictitious force is a force that appears to act on a mass whose motion is described using a non-inertial frame of reference such as a linearly accelerating or rotating reference frame. The moment of inertia otherwise known as the mass moment of inertia angular mass second moment of mass or most accurately rotational inertia of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis akin to how mass determines the force needed for a desired accelerationIt depends on the bodys mass.
Dynamics and kinematicsDynamics is general since the momenta forces and energy of the particles are taken into account. A non-inertial reference frame is a frame of reference that undergoes acceleration with respect to an inertial frame. The stationary-action principle also known as the principle of least action is a variational principle that when applied to the action of a mechanical system yields the equations of motion for that system.
Assuming SI units F is measured in newtons N m 1 and m 2 in kilograms kg r in meters m and the constant G is 6674 30 15 10 11 m 3 kg 1 s 2. 15 April 1707 18 September 1783 was a Swiss mathematician physicist astronomer geographer logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory complex analysis and infinitesimal. Leonhard Euler ˈ ɔɪ l ər OY-lər German.
However if the particles trajectory lies in a single plane it is sufficient to discard the vector nature of angular momentum and treat it as a scalar more precisely a pseudoscalar. The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798 although Cavendish did not himself calculate a numerical. Joseph-Louis Lagrange born Giuseppe Luigi Lagrangia or Giuseppe Ludovico De la Grange Tournier.
One observers state of rest is another observers state of uniform motion in a straight line and no experiment can deem either point of view to be correct or incorrect. These were developed intensively from the second half of the 18th century by for example DAlembert Euler and Lagrange until the 1930s. An accelerometer at rest in a non-inertial frame will in general detect a non-zero acceleration.
For an N particle system in 3 dimensions there are 3N second order ordinary differential equations in the positions of the particles to solve for. Instead of forces Lagrangian mechanics uses the energies in the system. Applies to each particle.
Motion is mathematically described in terms of displacement distance velocity acceleration speed and frame of reference to an observer and measuring the change in position of the body relative to that frame with change in time. The idea of a constraint is useful - since this limits what the system can do and can. Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change.
While the laws of motion are the same in all inertial frames in non-inertial frames they vary from frame to frame depending on the acceleration. Sir William Rowan Hamilton LLD DCL MRIA FRAS 34 August 1805 2 September 1865 was an Irish mathematician astronomer and physicist. ʒɑ batist lə ʁɔ dalɑbɛːʁ.
This principle states that infinitesimal virtual work done by a force across reversible displacements is zero which is the work done by a force consistent with ideal constraints of the system. The principle expressed by Newtons first law is that there is no way to say which inertial observer is really moving and which is really standing still. The foundation which the subject is built on is DAlemberts principle.
In physics motion is the phenomenon in which an object changes its position with respect to time. The central quantity of Lagrangian mechanics is the Lagrangian a function which summarizes the dynamics of. DAlemberts form of the principle of virtual work.
The principle states that the trajectories ie. The branch of physics describing the. The solutions of the equations of motion are stationary points of the systems action functional.
Jean-Baptiste le Rond dAlembert d æ l ə m ˈ b ɛər. It is related to Newtons second law of motion which treats forces for just one object. After some other definitions Newton states in his first law of motion.
21 June 14 November 1716 was a German polymath active as a mathematician philosopher scientist and diplomatHe is one of the most prominent figures in both the history of philosophy and the history of mathematicsHe wrote works on philosophy theology ethics politics law history and philology. In physics Liouvilles theorem named after the French mathematician Joseph Liouville is a key theorem in classical statistical and Hamiltonian mechanicsIt asserts that the phase-space distribution function is constant along the trajectories of the systemthat is that the density of system points in the vicinity of a given system point traveling through phase-space is constant. The equations of motion for a mechanical system of rigid bodies can be determined using DAlemberts form of the principle of virtual work.
Gottfried Wilhelm von Leibniz 1 July 1646 OS. He solves these examples and others. Mass is an intrinsic property of a body.
Where F is the force m 1 and m 2 are the masses of the objects interacting r is the distance between the centers of the masses and G is the gravitational constant. The theory of partial differential equation variational calculus Fourier analysis potential theory and vector analysis are perhaps most closely associated with mathematical physics. In all these cases y is an unknown function of x or of x 1 and x 2 and f is a given function.
He was the Andrews Professor of Astronomy at Trinity College Dublin and Royal Astronomer of Ireland living at Dunsink Observatory. Spelled out as pi is a mathematical constant that is the ratio of a circles circumference to its diameter approximately equal to 314159The number π appears in many formulas across mathematics and physicsIt is an irrational number meaning that it cannot be expressed exactly as a ratio of two integers although fractions such as are commonly used to.

D Alembert S Principle And Lagrange S Equations Youtube

Lec 9 Lagrange Equation From D Alembert S Principle Youtube

D Alembert S Principle And Applications Pdf Free Download

Lambert W Function Wikipedia

D Alembert S Principle And Applications Pdf Free Download

D Alembert Principle And Lagrange S Equations Pdf Scientific Theories Force

Solved Problems 47 Problem 2 2 Use D Alembert S Principle Chegg Com

Physics 319 Classical Mechanics Ppt Download

Lambert W Function Wikipedia

Ppt Sect 1 4 D Alembert S Principle Lagrange S Eqtns Powerpoint Presentation Id 937153
Lagrange Multiplier In Hamilton S And D Alembert S Principles Physics Forums

Pdf Lagrange S Equations Derived From D Alembert S Principle Mrigendra Basukinandan F Anisam Academia Edu

Derivation Of Lagrange Equations From D Alembert Pdf Lagrangian Mechanics Force

D Alembert S Principle And Lagrange S Equations Youtube

Laboratoire De Recherche En Informatique 2005 2008 Report Lri
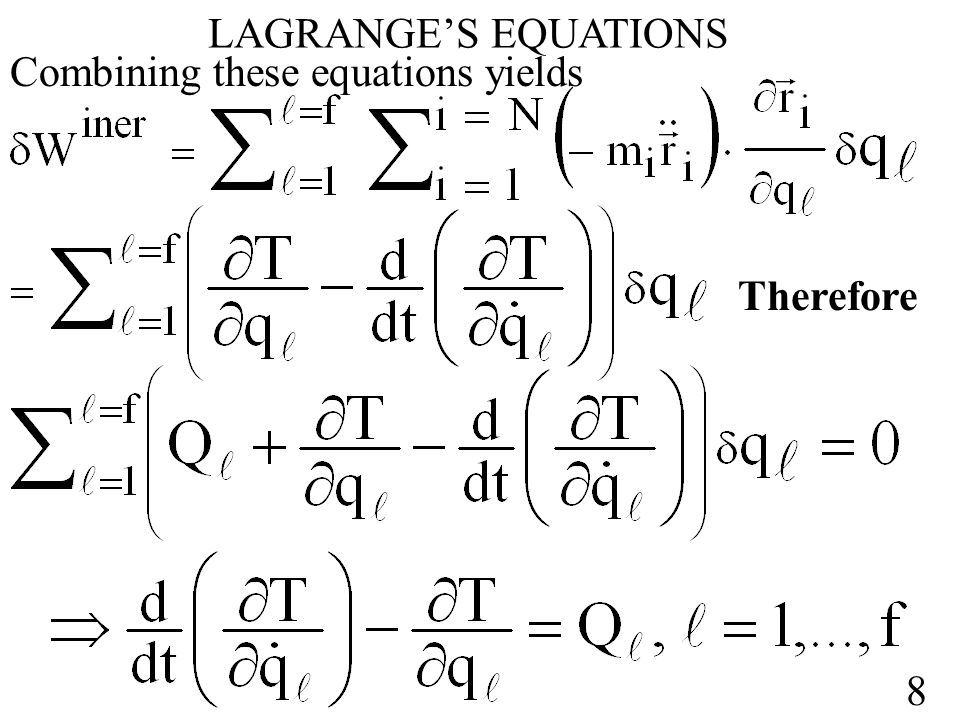
D Alembert S Principle The Sum Of The Work Done By Ppt Video Online Download

Lambert W Function Wikipedia